pacman::p_load(sf, sfdep, tmap, tidyverse)In-class Exercise 2: Global and Local Measures of Spatial Association - sfdep methods
Getting started
Installing and Loading the R Packages
Importing geospatial data
hunan <- st_read(dsn = "data/geospatial",
layer = "Hunan")Reading layer `Hunan' from data source
`D:\zzc\ISSS624\In-class_EX\In-class_EX2\data\geospatial' using driver `ESRI Shapefile'
Simple feature collection with 88 features and 7 fields
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: 108.7831 ymin: 24.6342 xmax: 114.2544 ymax: 30.12812
Geodetic CRS: WGS 84Importing attribute table
hunan2012 <- read_csv("data/aspatial/Hunan_2012.csv")Rows: 88 Columns: 29
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (2): County, City
dbl (27): avg_wage, deposite, FAI, Gov_Rev, Gov_Exp, GDP, GDPPC, GIO, Loan, ...
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.Combining both data frame by using left join
hunan_GDPPC <- left_join(hunan, hunan2012) %>%
select(1:4, 7, 15)Joining with `by = join_by(County)`Plotting a choropleth map
tmap_mode("plot")tmap mode set to plottingtm_shape(hunan_GDPPC) +
tm_fill("GDPPC",
style = "quantile",
palette = "Blues",
title = "GDPPC") +
tm_layout(main.title = "Distribution of GDP per capita by district, Hunan Province",
main.title.position = "center",
main.title.size = 1.2,
legend.height = 0.45,
legend.width = 0.35,
frame = TRUE) +
tm_borders(alpha = 0.5) +
tm_compass(type="8star", size = 2) +
tm_scale_bar() +
tm_grid(alpha =0.2)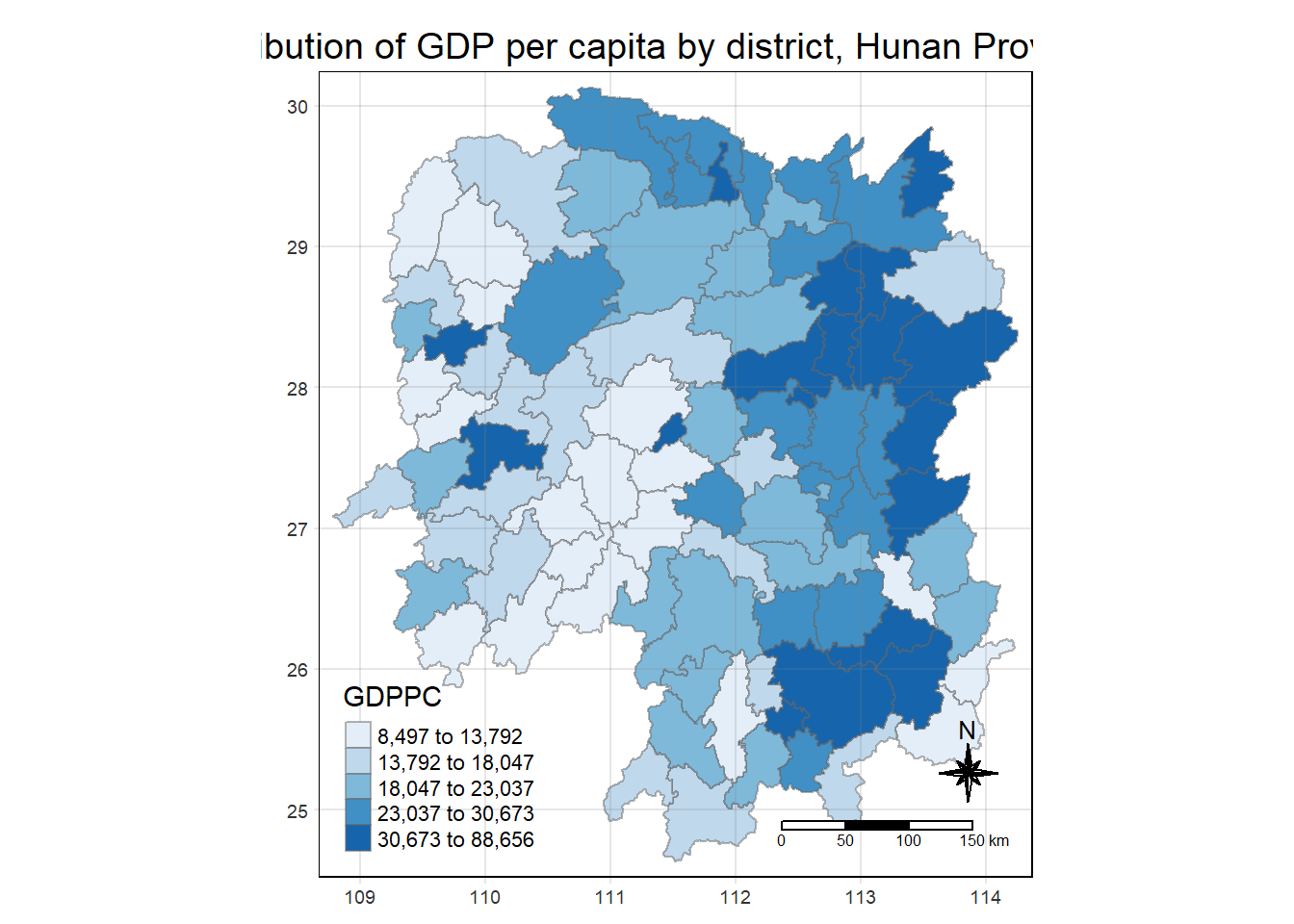
Global Measures of Spatial Association
Step 1: Deriving contiguity weights: Queen’s method
Deriving contiguity weights: Queen’s method
wm_q <- hunan_GDPPC %>%
mutate(nb = st_contiguity(geometry),
wt = st_weights(nb,
style = "W"),
.before = 1) wm_qSimple feature collection with 88 features and 8 fields
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: 108.7831 ymin: 24.6342 xmax: 114.2544 ymax: 30.12812
Geodetic CRS: WGS 84
First 10 features:
nb
1 2, 3, 4, 57, 85
2 1, 57, 58, 78, 85
3 1, 4, 5, 85
4 1, 3, 5, 6
5 3, 4, 6, 85
6 4, 5, 69, 75, 85
7 67, 71, 74, 84
8 9, 46, 47, 56, 78, 80, 86
9 8, 66, 68, 78, 84, 86
10 16, 17, 19, 20, 22, 70, 72, 73
wt
1 0.2, 0.2, 0.2, 0.2, 0.2
2 0.2, 0.2, 0.2, 0.2, 0.2
3 0.25, 0.25, 0.25, 0.25
4 0.25, 0.25, 0.25, 0.25
5 0.25, 0.25, 0.25, 0.25
6 0.2, 0.2, 0.2, 0.2, 0.2
7 0.25, 0.25, 0.25, 0.25
8 0.1428571, 0.1428571, 0.1428571, 0.1428571, 0.1428571, 0.1428571, 0.1428571
9 0.1666667, 0.1666667, 0.1666667, 0.1666667, 0.1666667, 0.1666667
10 0.125, 0.125, 0.125, 0.125, 0.125, 0.125, 0.125, 0.125
NAME_2 ID_3 NAME_3 ENGTYPE_3 County GDPPC
1 Changde 21098 Anxiang County Anxiang 23667
2 Changde 21100 Hanshou County Hanshou 20981
3 Changde 21101 Jinshi County City Jinshi 34592
4 Changde 21102 Li County Li 24473
5 Changde 21103 Linli County Linli 25554
6 Changde 21104 Shimen County Shimen 27137
7 Changsha 21109 Liuyang County City Liuyang 63118
8 Changsha 21110 Ningxiang County Ningxiang 62202
9 Changsha 21111 Wangcheng County Wangcheng 70666
10 Chenzhou 21112 Anren County Anren 12761
geometry
1 POLYGON ((112.0625 29.75523...
2 POLYGON ((112.2288 29.11684...
3 POLYGON ((111.8927 29.6013,...
4 POLYGON ((111.3731 29.94649...
5 POLYGON ((111.6324 29.76288...
6 POLYGON ((110.8825 30.11675...
7 POLYGON ((113.9905 28.5682,...
8 POLYGON ((112.7181 28.38299...
9 POLYGON ((112.7914 28.52688...
10 POLYGON ((113.1757 26.82734...Computing Global Moran’ I
moranI <- global_moran(wm_q$GDPPC,
wm_q$nb,
wm_q$wt)
glimpse(moranI)List of 2
$ I: num 0.301
$ K: num 7.64Performing Global Moran’sI test
global_moran_test(wm_q$GDPPC,
wm_q$nb,
wm_q$wt)
Moran I test under randomisation
data: x
weights: listw
Moran I statistic standard deviate = 4.7351, p-value = 1.095e-06
alternative hypothesis: greater
sample estimates:
Moran I statistic Expectation Variance
0.300749970 -0.011494253 0.004348351 Performing Global Moran’I permutation test
set.seed(1234)global_moran_perm(wm_q$GDPPC,
wm_q$nb,
wm_q$wt,
nsim = 99)
Monte-Carlo simulation of Moran I
data: x
weights: listw
number of simulations + 1: 100
statistic = 0.30075, observed rank = 100, p-value < 2.2e-16
alternative hypothesis: two.sidedComputing local Moran’s I
lisa <- wm_q %>%
mutate(local_moran = local_moran(
GDPPC, nb, wt, nsim = 99),
.before = 1) %>%
unnest(local_moran)Visualising local Moran’s I
tmap_mode("plot")tmap mode set to plottingtm_shape(lisa) +
tm_fill("ii") +
tm_borders(alpha = 0.5) +
tm_view(set.zoom.limits = c(6,8)) +
tm_layout(main.title = "local Moran's I of GDPPC",
main.title.size = 0.8)Variable(s) "ii" contains positive and negative values, so midpoint is set to 0. Set midpoint = NA to show the full spectrum of the color palette.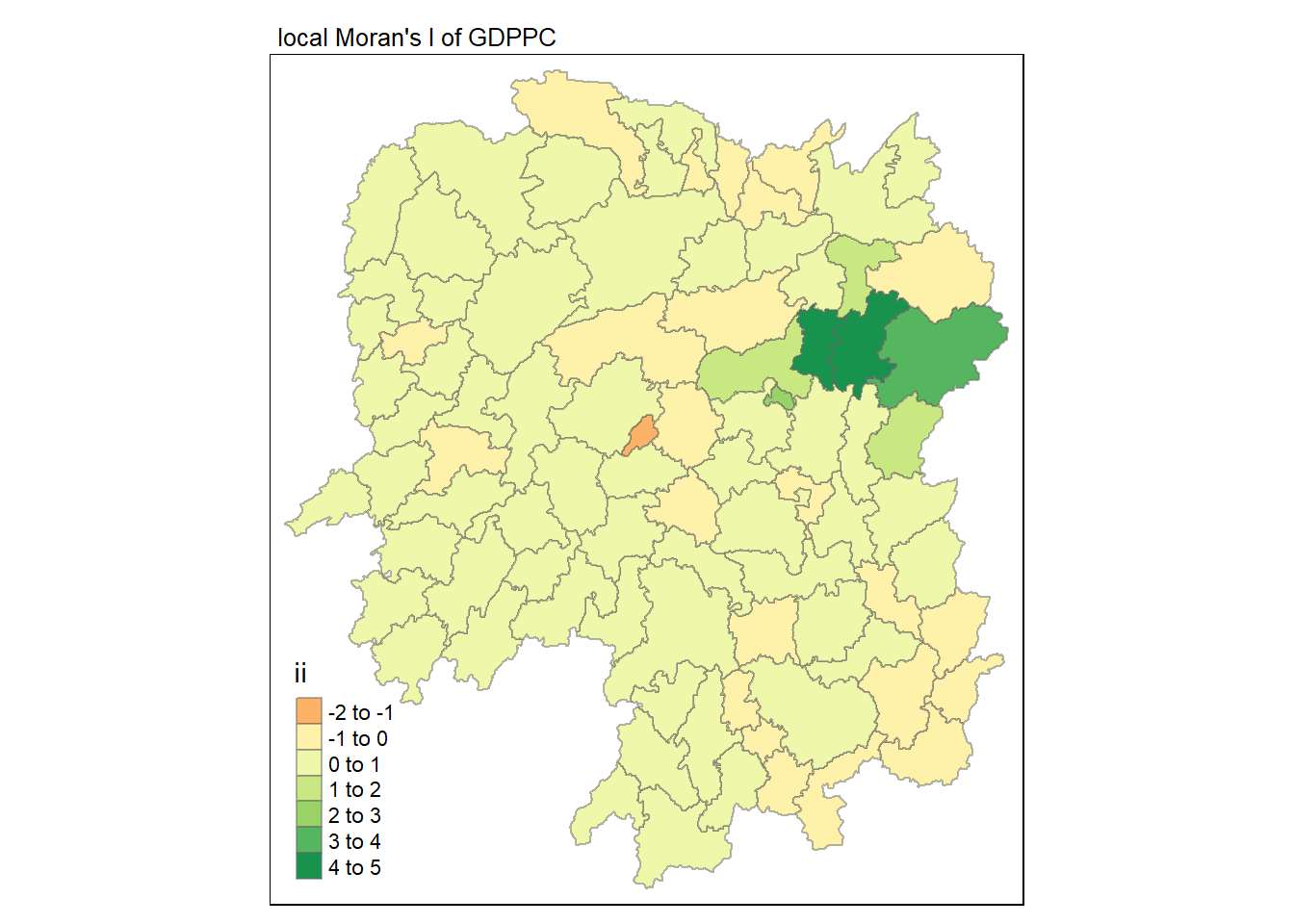
Visualising p-value of local Moran’s I
tmap_mode("plot")tmap mode set to plottingtm_shape(lisa) +
tm_fill("p_ii_sim") +
tm_borders(alpha = 0.5) +
tm_layout(main.title = "p-value of local Moran's I",
main.title.size = 0.8)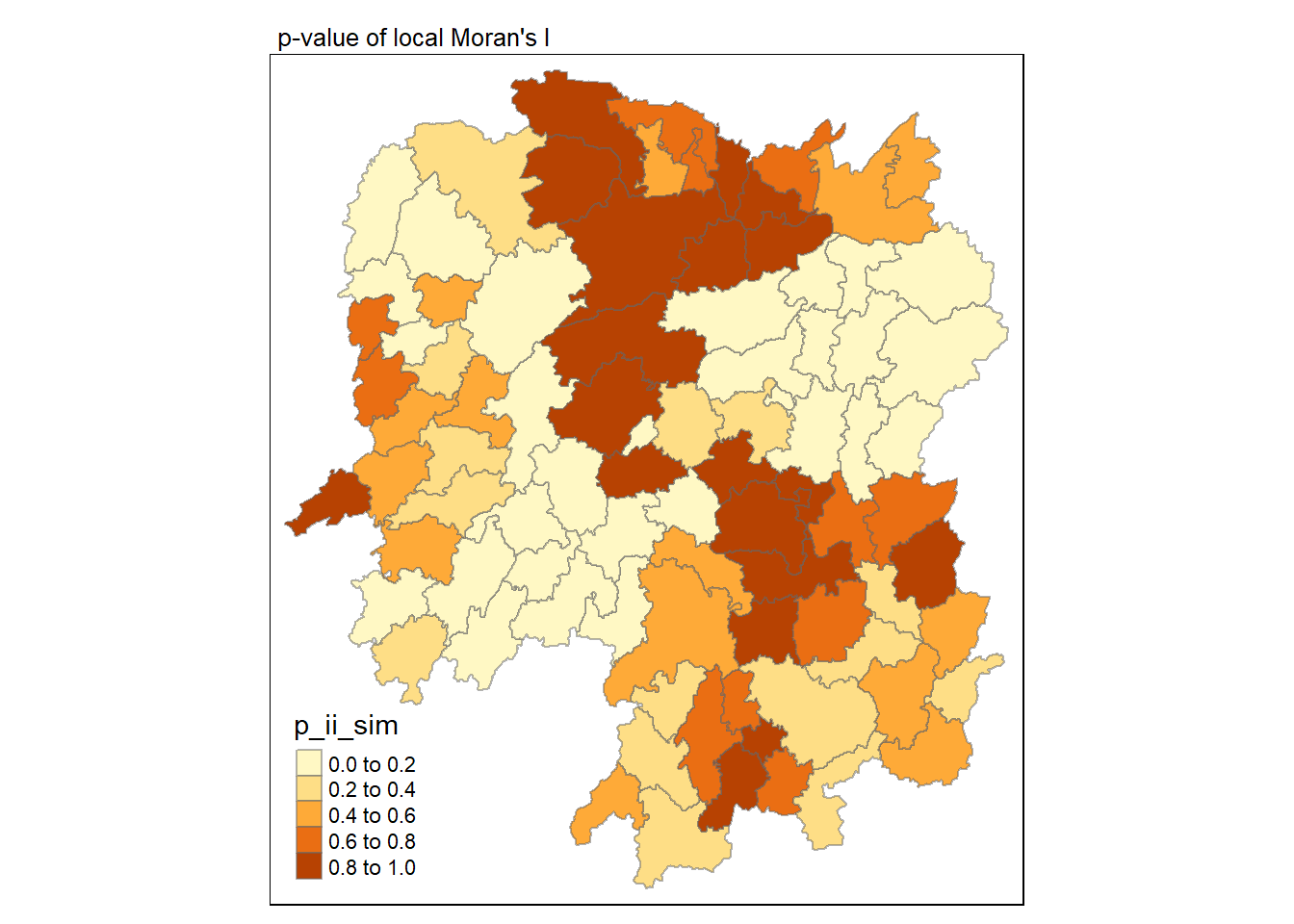
Visuaising local Moran’s I and p-value
tmap_mode("plot")tmap mode set to plottingmap1 <- tm_shape(lisa) +
tm_fill("ii") +
tm_borders(alpha = 0.5) +
tm_view(set.zoom.limits = c(6,8)) +
tm_layout(main.title = "local Moran's I of GDPPC",
main.title.size = 0.8)
map2 <- tm_shape(lisa) +
tm_fill("p_ii",
breaks = c(0, 0.001, 0.01, 0.05, 1),
labels = c("0.001", "0.01", "0.05", "Not sig")) +
tm_borders(alpha = 0.5) +
tm_layout(main.title = "p-value of local Moran's I",
main.title.size = 0.8)
tmap_arrange(map1, map2, ncol = 2)Variable(s) "ii" contains positive and negative values, so midpoint is set to 0. Set midpoint = NA to show the full spectrum of the color palette.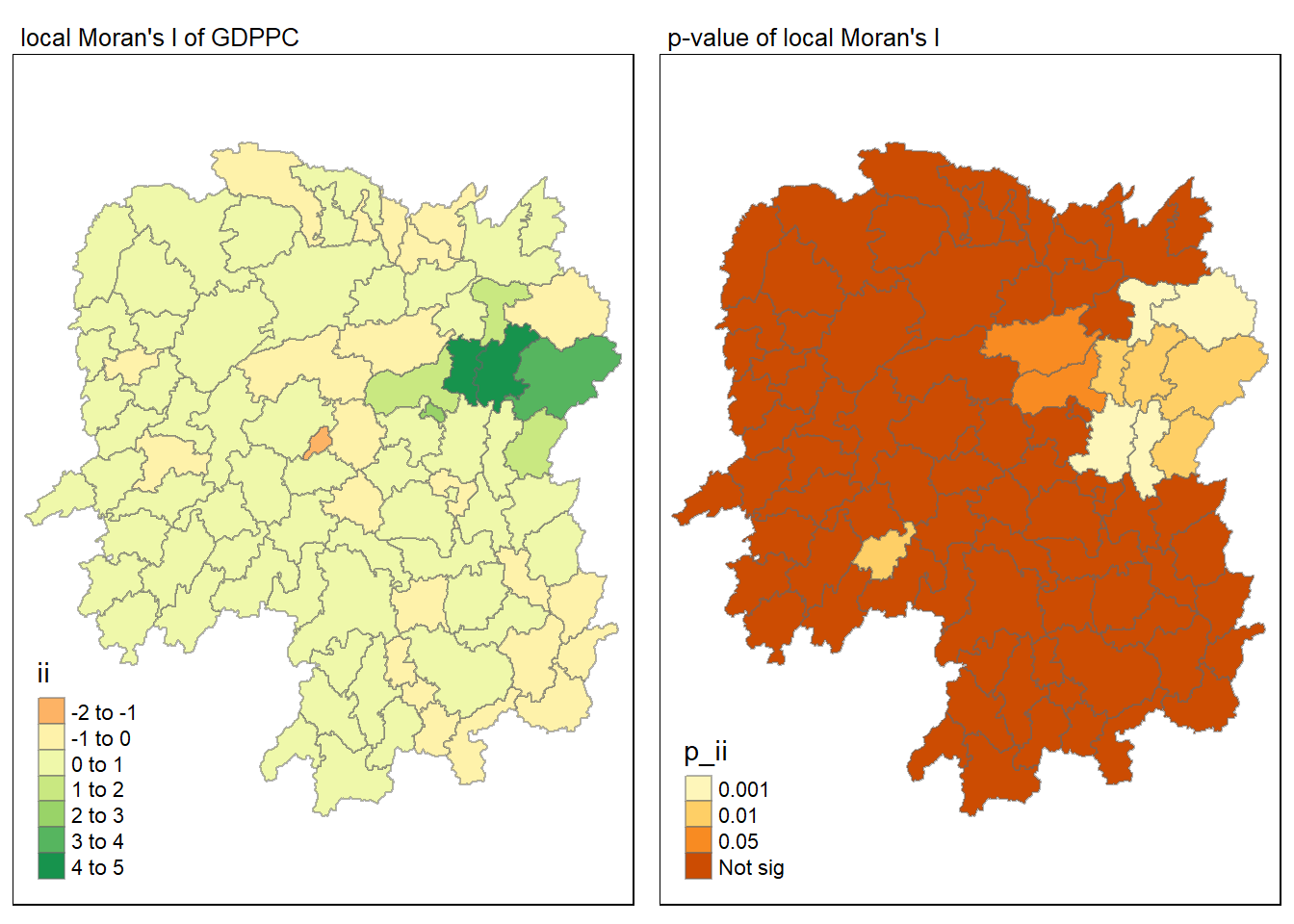
Visualising LISA map
lisa_sig <- lisa %>%
filter(p_ii < 0.05)
tmap_mode("plot")tmap mode set to plottingtm_shape(lisa) +
tm_polygons() +
tm_borders(alpha = 0.5) +
tm_shape(lisa_sig) +
tm_fill("mean") +
tm_borders(alpha = 0.4)Warning: One tm layer group has duplicated layer types, which are omitted. To
draw multiple layers of the same type, use multiple layer groups (i.e. specify
tm_shape prior to each of them).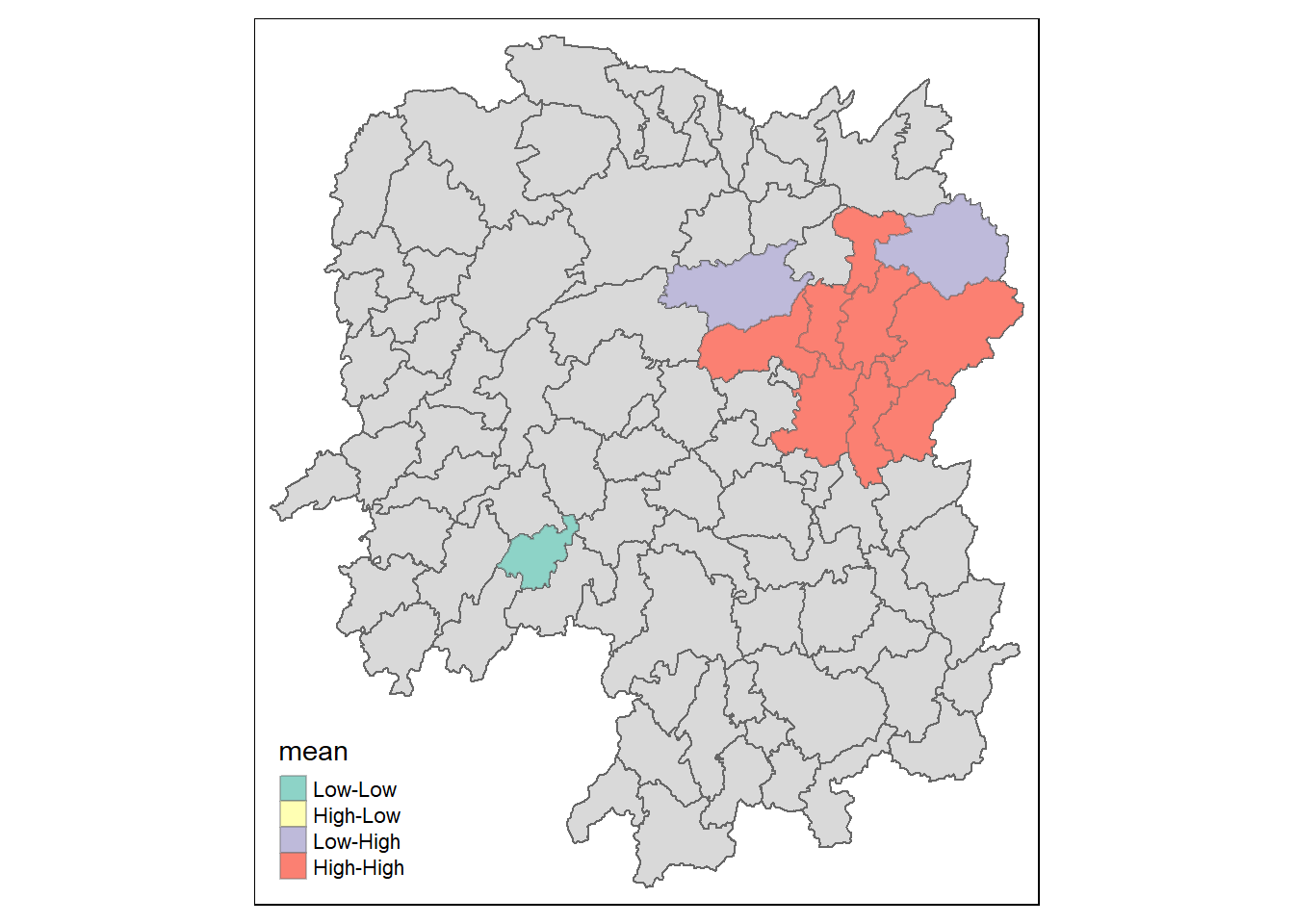
Hot Spot and Cold Spot Area Analysis (HCSA)
Computing local Gi* statistics
wm_idw <- hunan_GDPPC %>%
mutate(nb = st_contiguity(geometry),
wts = st_inverse_distance(nb, geometry,
scale = 1,
alpha = 1),
.before = 1)! Polygon provided. Using point on surface.Warning: There was 1 warning in `stopifnot()`.
ℹ In argument: `wts = st_inverse_distance(nb, geometry, scale = 1, alpha = 1)`.
Caused by warning in `st_point_on_surface.sfc()`:
! st_point_on_surface may not give correct results for longitude/latitude dataHCSA <- wm_idw %>%
mutate(local_Gi = local_gstar_perm(
GDPPC, nb, wt, nsim = 99),
.before = 1) %>%
unnest(local_Gi)
HCSASimple feature collection with 88 features and 16 fields
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: 108.7831 ymin: 24.6342 xmax: 114.2544 ymax: 30.12812
Geodetic CRS: WGS 84
# A tibble: 88 × 17
gi_star e_gi var_gi p_value p_sim p_folded_sim skewness kurtosis nb
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <nb>
1 0.0416 0.0114 6.41e-6 0.0493 9.61e-1 0.7 0.35 0.875 <int>
2 -0.333 0.0106 3.84e-6 -0.0941 9.25e-1 1 0.5 0.661 <int>
3 0.281 0.0126 7.51e-6 -0.151 8.80e-1 0.9 0.45 0.640 <int>
4 0.411 0.0118 9.22e-6 0.264 7.92e-1 0.6 0.3 0.853 <int>
5 0.387 0.0115 9.56e-6 0.339 7.34e-1 0.62 0.31 1.07 <int>
6 -0.368 0.0118 5.91e-6 -0.583 5.60e-1 0.72 0.36 0.594 <int>
7 3.56 0.0151 7.31e-6 2.61 9.01e-3 0.06 0.03 1.09 <int>
8 2.52 0.0136 6.14e-6 1.49 1.35e-1 0.2 0.1 1.12 <int>
9 4.56 0.0144 5.84e-6 3.53 4.17e-4 0.04 0.02 1.23 <int>
10 1.16 0.0104 3.70e-6 1.82 6.86e-2 0.12 0.06 0.416 <int>
# ℹ 78 more rows
# ℹ 8 more variables: wts <list>, NAME_2 <chr>, ID_3 <int>, NAME_3 <chr>,
# ENGTYPE_3 <chr>, County <chr>, GDPPC <dbl>, geometry <POLYGON [°]>Visualising Gi*
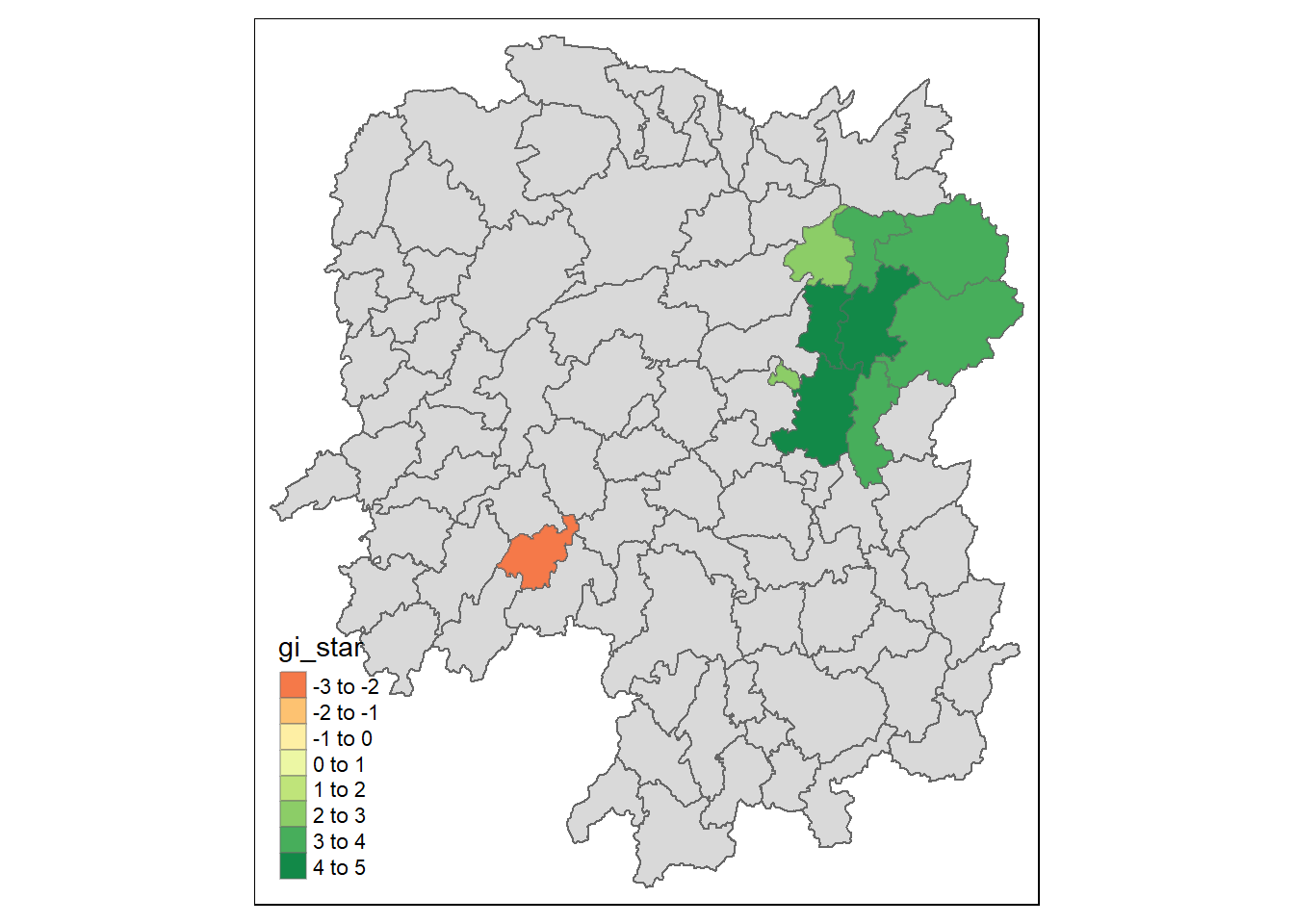
tmap_mode("plot")tmap mode set to plottingtm_shape(HCSA) +
tm_fill("gi_star") +
tm_borders(alpha = 0.5) +
tm_view(set.zoom.limits = c(6,8))Variable(s) "gi_star" contains positive and negative values, so midpoint is set to 0. Set midpoint = NA to show the full spectrum of the color palette.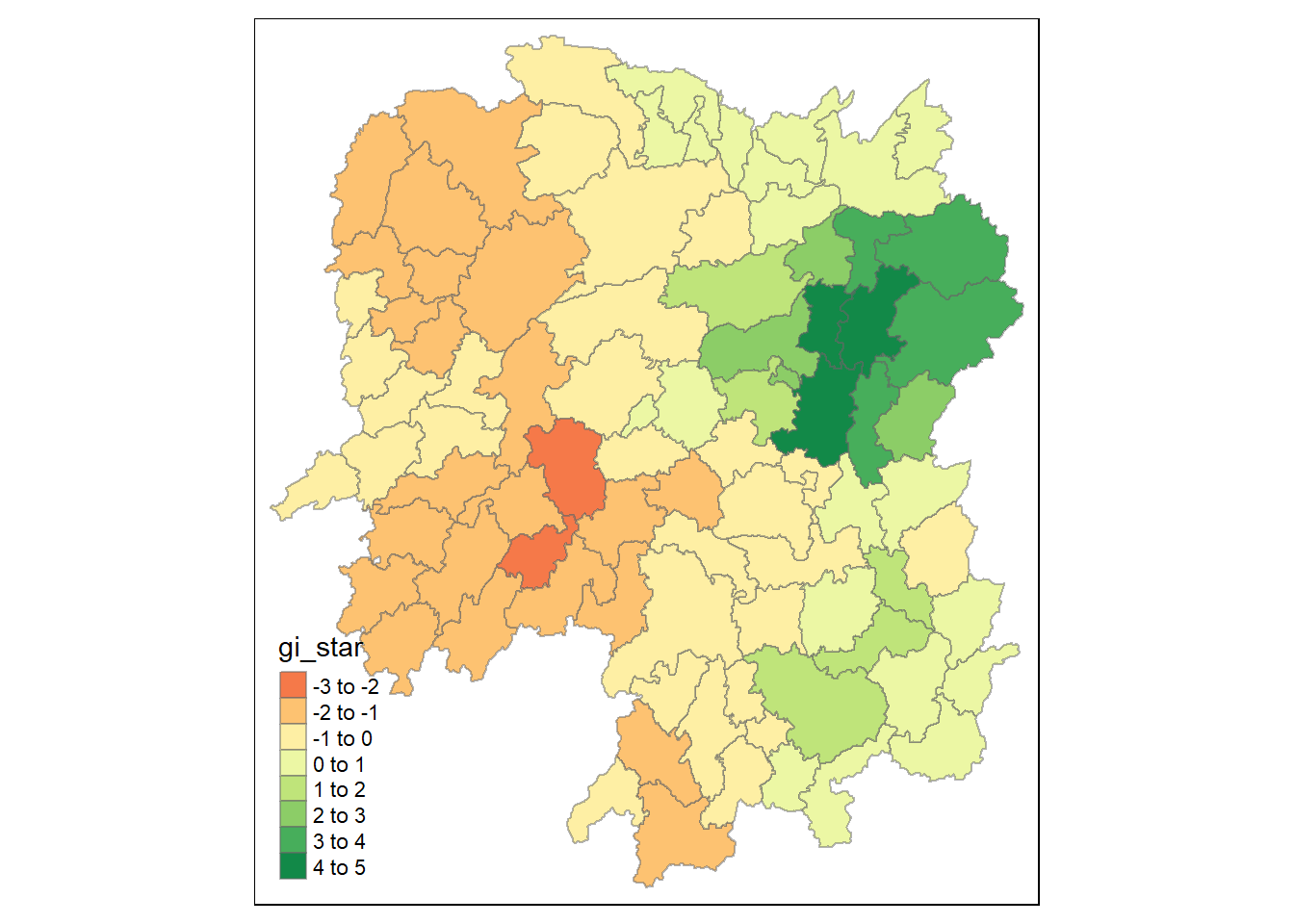
Visualising p-value of HCSA
tmap_mode("plot")tmap mode set to plottingtm_shape(HCSA) +
tm_fill("p_sim") +
tm_borders(alpha = 0.5)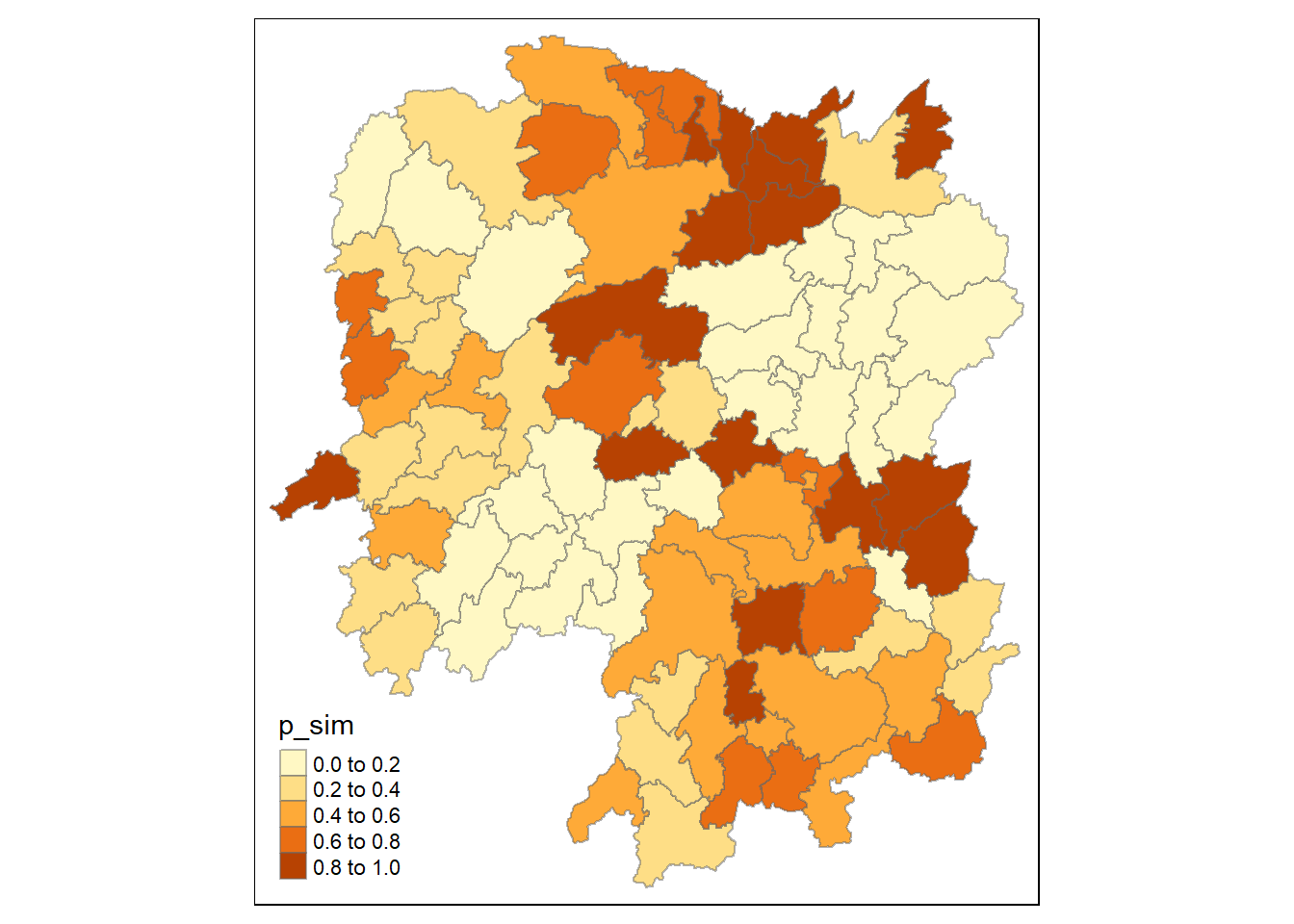
Visuaising local HCSA
tmap_mode("plot")tmap mode set to plottingmap1 <- tm_shape(HCSA) +
tm_fill("gi_star") +
tm_borders(alpha = 0.5) +
tm_view(set.zoom.limits = c(6,8)) +
tm_layout(main.title = "Gi* of GDPPC",
main.title.size = 0.8)
map2 <- tm_shape(HCSA) +
tm_fill("p_value",
breaks = c(0, 0.001, 0.01, 0.05, 1),
labels = c("0.001", "0.01", "0.05", "Not sig")) +
tm_borders(alpha = 0.5) +
tm_layout(main.title = "p-value of Gi*",
main.title.size = 0.8)
tmap_arrange(map1, map2, ncol = 2)Variable(s) "gi_star" contains positive and negative values, so midpoint is set to 0. Set midpoint = NA to show the full spectrum of the color palette.Warning: Values have found that are less than the lowest breakWarning: Values have found that are higher than the highest breakVariable(s) "p_value" contains positive and negative values, so midpoint is set to 0. Set midpoint = NA to show the full spectrum of the color palette.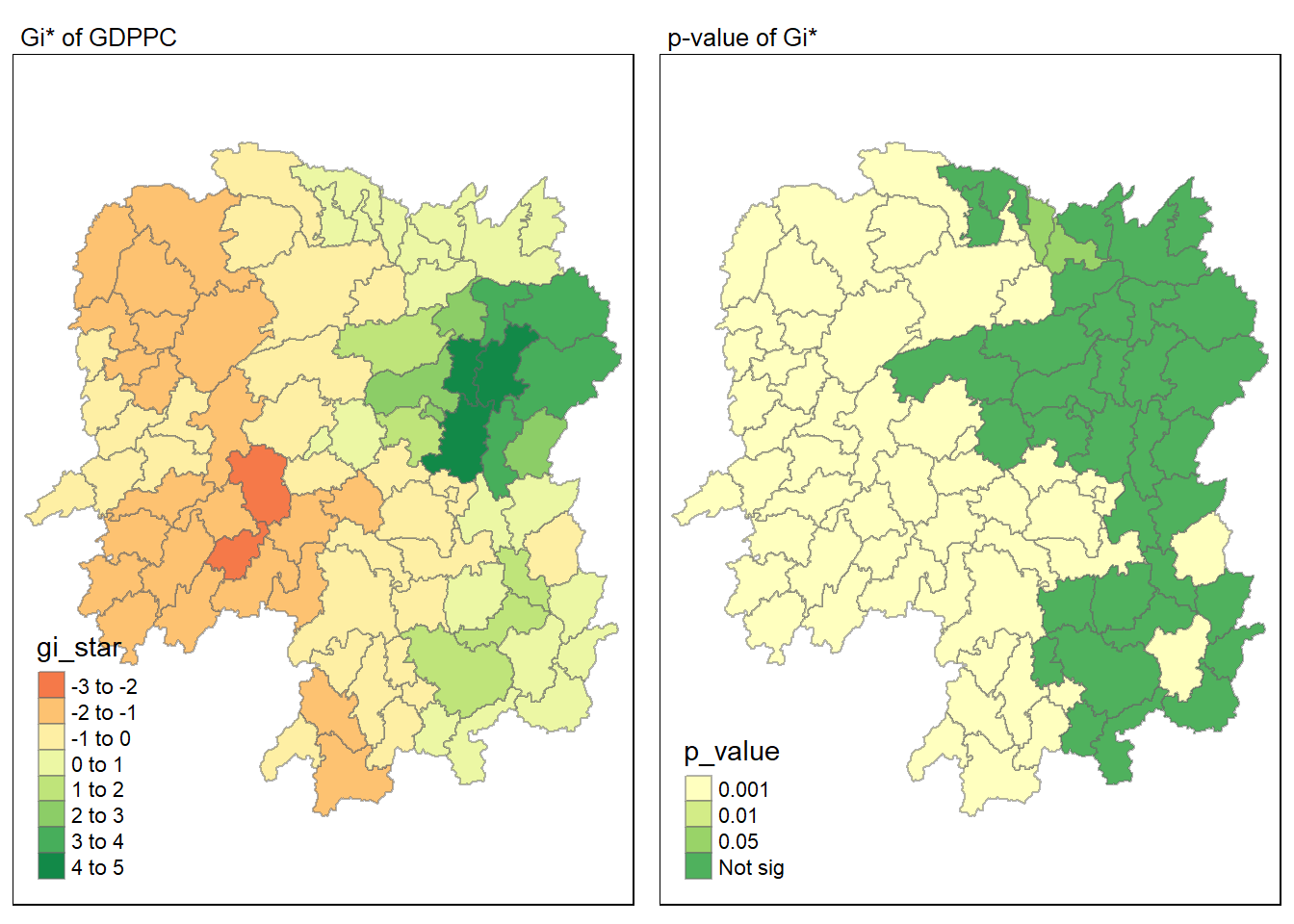
Visualising hot spot and cold spot areas
HCSA_sig <- HCSA %>%
filter(p_sim < 0.05)
tmap_mode("plot")tmap mode set to plottingtm_shape(HCSA) +
tm_polygons() +
tm_borders(alpha = 0.5) +
tm_shape(HCSA_sig) +
tm_fill("gi_star") +
tm_borders(alpha = 0.4)Warning: One tm layer group has duplicated layer types, which are omitted. To
draw multiple layers of the same type, use multiple layer groups (i.e. specify
tm_shape prior to each of them).Variable(s) "gi_star" contains positive and negative values, so midpoint is set to 0. Set midpoint = NA to show the full spectrum of the color palette.